Published on the World Wide Web, September 8,
1997.
Revised October 26, 1997
Edited by Charles H. Bucknam
The idea of using a simplified quantitative risk analysis (SQRA) for ore control sampling was developed to fulfill a need to economically justify improvements in field sampling practices. In the laboratory, the analytical chemist has excellent control over the reproducibility of the testing procedures, by requiring that the submitter of samples properly collect and prepare ore samples and present them for chemical analysis as finely ground powders (100-200 mesh). If gold ores contain finely disseminated gold particles, sampling is usually not a big problem in the laboratory and can be controlled to ~5% relative standard deviation (RSD).
The gold sampling theory of Pierre Gy predicts that the sampling variance (relative standard deviation ratio) is related to the the weight of the sub-sample in accordance with the following equation, assuming the sample is small compared to the ore block to be represented by the sample.
where:
M s = Sample Weight, g,
IH L = Gy Constant of
Heterogeneity1 ,
and
RSD =
Relative
Standard Deviation Ratio.
The sample weight is relatively easy to measure, but the variance and constant terms are a bit more elusive. The variance term in this equation is related to the fundamental error in sampling or "nugget effect" and is not always easy to isolate, because it is only part of the overall error in sampling and analysis. For this reason, it is necessary to try to estimate the constant of heterogeneity, in order to predict the variance due to the fundamental error in sampling.
For Carlin type finely disseminated gold ores, I have used the atomic cloud model approximation. This approximation assumes that the ore is easy to sample because the gold is evenly distributed in the rock, as individual atoms. In this case, the liberation of the gold may be approximated by spherical particles with a liberation size of 3 angstroms or 0.00000003 cm. This is the limiting case for gold liberation. The constant of heterogeneity for collecting samples from nominal 2-cm blast hole cuttings for a 3 g Au/t gold deposit using the atomic cloud model is calculated using the following equation:
where:
IHL = Gy Constant of Heterogeneity (696),
f = Shape Factor
(0.5
for a sphere),
g = granulometric factor (0.25 for broken ore),
c = mineralogic factor (19/0.000003=6333333 for 3 g Au/t)
l = liberation factor ((0.00000003/2)^0.5=0.000122 for 3 A at
2-cm), and
d = 95% passing particle size (2), cm.
For this example, assume that we wanted to calculate the variability due to the fundamental error in sampling for a nominal 8 kg sample weight. Rearranging the first equation yields:
To calculate the required sample weight to achieve the 15% RSD routine variability specification recommended by F. F. Pitard, proceed as follows:
Results from these preliminary calculations suggest that it will be necessary to collect a field sample weight which is larger than could be reasonably expected to be handled on a routine basis, manually. These results are typical for theoretical calculations based on gold liberation estimates, applied to field conditions. Gold liberation models work reasonably well for finely disseminated ores at particle sizes of 10 mesh or finer, but development of optimum sampling models for coarser ores usually requires conducting an empirical heterogeneity study.
At this point we have reached the limit of what can be accomplished in a desk study and need to perform some experimental work in order to find the optimum field sampling procedure. Who is going to pay for this work? What benefit will the gold mining operation gain by improved sampling? How will you be able to sell this to management? To answer these questions, the technique of simplified quantitative risk analysis was developed for application to ore control sampling.
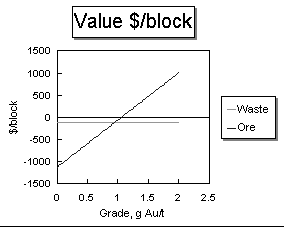
In order to build an economic justification for improved sampling, we must first start with an ore control economic model. This model is based on the cost of processing a mined block represented by an assay value as ore or waste and the revenue that would be generated if the block is processed as ore. For the purposes of demonstration we make the following assumptions:
The economic model is defined by the following equations:
where:
Vw = Value of Waste (-112.5), $/block
Cw
= Cost of Waste Haulage (0.75), $/ton
Tb = Tons per Mined
Block (150)
Vo = Value of Ore, $/block
Co =
Cost of Ore Processing (7.50), $/ton
Ro = Recovery of Gold
from Ore(0.75), Ratio
Go = Grade of Ore, g Au/t
0.02917 =
Conversion from g Au/t to oz Au/st
Vg = Value of Gold (325),
$/oz
Based on this information, an economic model may be calculated and plotted for mined blocks as a function of gold grade. The cut-off grade is the point where the two lines cross. The value of ore and waste are equal at this point, so the cut-off grade (0.95 g Au/t) can be calculated by the following equation:
G o = ( Co - Cw ) / ( Ro
*0.02917 * Vg ) = 0.95
If variability did not play a role in ore classification, the optimum economic model would classify all blocks assaying below the cut-off as waste and all off the blocks assaying above the cut-off as ore. In reality, however, there is a probability that the mined blocks will not be properly classified near the cut-off grade, which is a function of the number of standard deviations the assay for the block is from the cut-off grade. Simplified quantitative risk analysis (SQRA) uses this statistical relationship to demonstrate the potential economic benefits from improved sampling.
SQRA assumes that there is a normal error curve superimposed on the assay value for the mined block and that a portion of that curve is cut by the cut-off grade. The area under the normal curve below the cut-off grade is related to the probability that the block will be classified as waste and the area under the curve above the cut-off grade is related to the probability the block will be classified as ore. Thus, at the cut-off grade, there is a 50:50 probability that the block will be classified as ore or waste.
The probability ratios are multiplied the ore and waste economic models in order to apply quantitative risk assessment techniques2 to the economic value of the mined block and the results summed, in the "grey" area near the cut-off grade. The grade zone used for probability calculation is limited to a 5%-95% probability, for purposes of simplicity, and outside this grade zone ore and waste probability values of 0 and 1 are used. The SQRA ore control model equation is as follows :
where:
Vb = Value of Mined Block, $/block
Pw
= Probability of Block Classification as Waste, Ratio
Vw =
Value of Mined Block as Waste, $/block
Po = Probability of
Block Classification as Ore, Ratio
Vw = Value of Mined Block as
Ore, $/block
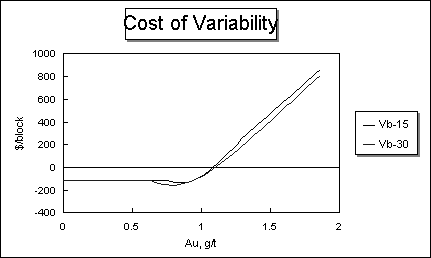
In order to obtain the probabilities, the value of z is calculated as the number of standard deviations that the assay value is from the cut-off grade. I have calculated the probabilities associated with the z values in a look-up table, so that they can be entered in a spreadsheet manually. The results for the 15% RSD and 30% RSD cases presented above, are shown in the figure below.

The variability causes the SQRA economic models to dip below the waste cost, due to the probability of ore being classified as waste, shifts the x intercept to higher grades,and reduces the slope with the 30% RSD case indicating higher losses of value than does the 15% RSD case. What is desired for justification of sampling improvements, however, is the differential added value for sampling improvements, which is calculated from the difference in the two curves, plotted below.
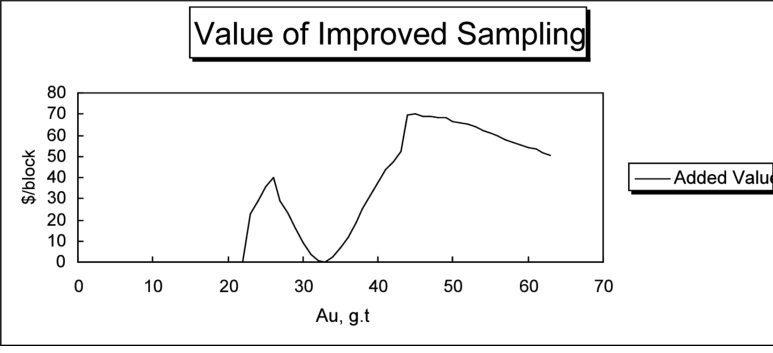
Typical sampling and assaying costs for an open pit gold mine might range $20-30 per sample. This plot shows that the potential for improvements in sampling ($70 max) have potential net benefits of up to several times the normal cost of sampling and assaying for blocks near the cut-off grade. To calculate the potential savings over the life of the mine, multiply the added value of each grade block by the modeled number of blocks of that grade for the deposit.
This procedure will provide the justification to carry out sampling studies, in order to develop the optimum sampling procedure for routine use in ore control. Always verify the results of the improved sampling procedure on several (~10) cuttings piles by comparing the routine sampling procedure to a reference method. The reference method would use metallurgical sample processing specifications (~5% RSD) which may require drying and crushing the entire cuttings pile to minus 10 mesh, bulk pulverizing a nominal 10 kg sub-sample and conducting an interlaboratory assaying study using at least 6 laboratories.
1 Pitard, F. F., Pierre Gy's Sampling Theory and Sampling Practice , CRC Press, 1991.
2 Roberds, W. J., " Environmental and Economic Risk Assessment/Management in Mine Development", presented to the SME Annual Meeting. Phoenix, Arizona, February 24-27, 1992, SME Preprint 92-149.
Return to: